NewFoS has a core of pioneers and experts in TA who are pushing research beyond the already extraordinary properties of TA waves, η, coherence, and robustness. For instance, NewFoS is investigating higher-order topological phenomena and extending current knowledge to include topological robustness in the presence of multiple degrees of freedom. We are also addressing open areas of research in nonlinear TA. By utilizing synthetic gauge fields and synthetic dimensions, NewFoS is advancing TA beyond current quantum physics analogies to drive new breakthroughs in coherence. These yet-unknown advances will serve as foundational resources for long-term technological development.
Hidden symmetry for topological phenomena
Lead by Andrea Alú, CUNY.
For instance, topological protection against scattering, a key property for the design of low loss TA wave devices, exploits (a) the orthogonality of counter-propagating waves resulting from breaking inversion symmetry of pseudospin TA waves, and (b) the absence of a counter-propagating waves resulting from breaking time-reversal symmetry of TA waves. While the second type of topologically protected wave is more robust than the first type, its practical physical implementation is more challenging due to the need to inject energy into the system. NewFoS will explore other symmetry breaking strategies (e.g., translational symmetry) to achieve robust immunity to backscattering in TA structures that can be realized in passive systems.
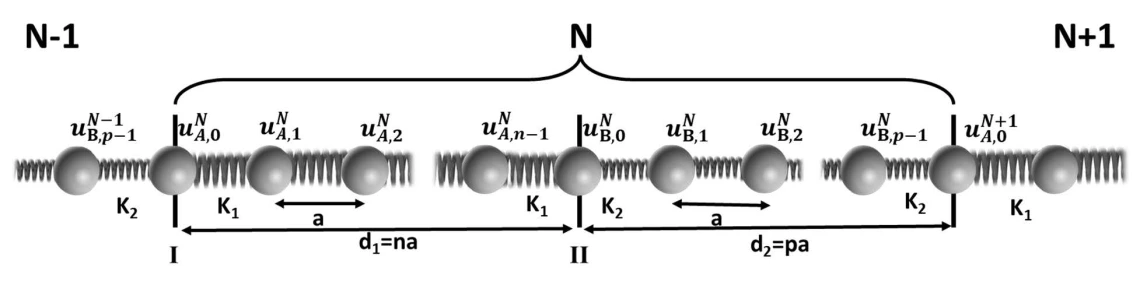
Schematic representation of a one-dimensional discrete superlattice. A periodically repeating unit cell N is composed of equally spaced identical unit masses coupled through linear springs with stiffnesses of K1 and K2.
Crystals 2024, 14(1), 92; https://doi.org/10.3390/cryst14010092
Effect of nonlinearity on topological properties
Lead by Chiara Daraio, Caltech.
Non-symmetry breaking topological order may arise in strongly correlated systems even if there is an apparent lack of long-range order as measured by local order parameters. This phenomenon has been essentially associated with topological order in quantum systems such as spin lattices. NewFoS will explore classical strongly correlated nonlinear acoustic systems that can lead to behaviors analogous to the quantum topological ordered phases. This research will open new avenues to investigating emergent topological phenomena resulting from nonlinear correlations. These phenomena will offer revolutionary paths to developing acoustic analogues of topological qubits and novel approaches to robust massively parallel information processing.
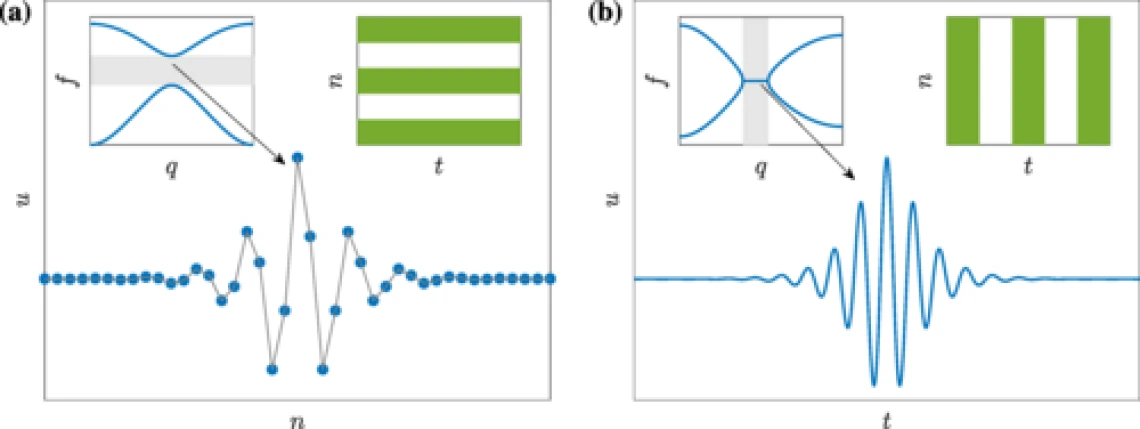
(a) Illustration of a classical discrete breather, which is localized in space and periodic in time. The linear spectrum is shown in the left inset, where the frequency f is plotted against the wavenumber q. The spectrum has a frequency gap, which is induced by the spatial periodicity of the medium. A schematic of the underlying medium is shown in the right inset. The frequency of the breather lies in the frequency gap (horizontal gray shaded region in the spectrum shown in the left inset). (b) Illustration of a wavenumber bandgap (q-gap) breather (the focus of the present paper), which is localized in time and periodic in space. The linear spectrum is shown in the left inset, where the frequency f is plotted against the wavenumber q. The spectrum has a wavenumber gap, which is induced by the temporal periodicity of the medium (right inset). The wavenumber of the breather lies in the q-gap (vertical gray shaded region in the spectrum shown in the left inset).
Phys. Rev. Research 6, 023045, https://doi.org/10.1103/PhysRevResearch.6.023045
High-sensitivity topological phenomena
Lead by Massimo Ruzzene, UCB.
Among the topological properties of sound that have recently been uncovered, a few have emerged that are highly sensitive to parametric changes of governing physical properties. Beyond phase, which is thoroughly explored in project 3, exceptional points generated by the introduction of balanced gain and loss have attracted significant interest for potential sensing applications. The use of exceptional points to develop new sensing modalities is an open area of research which can be explored in the context of NewFos. The investigation of changes in an acoustic cavity or in an acoustic medium can leverage the interrogation of exceptional points and can lead to new concepts of relevant to a variety of fields, such as assessment of the mechanical properties of cells, to the detection of damage or, more generally, heterogeneities in structural components. In addition, the study of acoustic waves generated by complex frequency excitation and their interaction with heterogeneities and impedance mismatched interfaces can be also studied in the context of topology, leading to analogies related to time inversion symmetries, PT symmetries and non-Hermitian dynamics. These investigations are also likely to lead to novel concepts for sensing and for new ultrasound imaging strategies.
Eigenfrequency study in COMSOL using PMLs to prevent reflections work from J. Lewton, K. Runge, P. A. Deymier and M. Ruzzene.